TrBlog
0%

leet code 每日三道题 01 array+binary search

Posted on Edited on In

leet code 每日三道题 01 array+binary search

29题 除法 M

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
package com.leetcode;

import java.util.Arrays;

public class DivideTwoIntegers {
    public static void main(String[] args) {
        System.out.println(solution.divideTwo(Integer.MIN_VALUE, Integer.MAX_VALUE));
    }

    /**
     * 问题：不使用 * / % 符号完成除法
     * <p>
     * 思路：1. 暴力算法，除法可以看作减法，每次减去被除数，当结果<0说明结束，但是这样会导致被除数为1的时候循环次数为被除数，会超时的
     * <p>
     * 思路：2. 首先位运算 除2：`>>1` 乘2：`<<1`。然后我们看整个除法表达式，比如 `13/4 = 3 ==> 13 = 4 * 3`
     * 换算成二进制：`1101 = 4 * 0010+ 4* 0001` 也就是4个 `0010`和`0001`，所以可以看出规律，那就是除法的结果必定为除数的倍数的二进制位。
     * <p>
     * 由此可以遍历二进制数（从 1000.. 遍历到 000..001），题目的最大是32位，现在假如最高8位，那么从最高位开始 `1000 0000 * 4 > 1010`
     * 循环直到发现`0010(2) * 4 < 1101`,记录下`0010`, 那么剩下是数就是 13-8=5 ,继续遍历`0001 * 4 < 5` 记录下`0001`，遍历结束，
     * 结果为 `0001 *4 + 0010 * 4` 即 `0001 + 0010 `（3） * 4 ，最后结果为 3。
     * <p>
     * 具体实现中，为了不使用乘法符号完成乘法，使用`<<`  比如 `0001`和`0010`分别乘4就是 4 和 4<<1，所以可以定义一个初始数组arr，
     * `arr[0]`放被除数，1,2,3 分别是前一位的乘2即<<1。
     */
    public static class solution {
        public static int divide(int dividend, int divisor) {
            if (dividend == Integer.MIN_VALUE && divisor == 1) return dividend;
            if (dividend == Integer.MIN_VALUE && divisor == -1) return Integer.MAX_VALUE;
            boolean isPos = (dividend > 0 && divisor > 0) || (dividend < 0 && divisor < 0);
//            boolean isMin = dividend == Integer.MIN_VALUE;
            long array[] = new long[32];
            long result = 0;
            divisor = Math.abs(divisor);
            long dividentInput = dividend;
            dividentInput = Math.abs(dividentInput);
            array[0] = divisor;
            int truePosi = 0;
            for (int i = 1; i < array.length; i++) {
                // 当前位都是前一位的*2 但是当tmp溢出的时候就可以停止了，两个正数的相除结果肯定是正数
                array[i] = array[i - 1] << 1;
                if (array[i] < 0) {
                    break;
                }
                truePosi = i;
            }
            // 从最高位开始遍历，做减法 1. 如果两个数为正 被除数减法，结果加法 2. 被除数为负， 结果加法，被除数加法
            for (int i = truePosi; i >= 0; i--) {
                if (array[i] <= dividentInput) {
                    // 假如 27位是结果 那么 27位应该是 array[27]/divisor 也就是 2的27次方
                    result += 1 << i;
                    dividentInput -= array[i];
                }
            }
            if (result > Integer.MAX_VALUE) result = Integer.MAX_VALUE;
            if (result < Integer.MIN_VALUE) result = Integer.MIN_VALUE;
            if (isPos) return (int) result;
            else return (int) -result;
        }

        /**
         * 除数 被除数 0：同为正，1：同为负号，异号（2：被除数正，除数负 3：被除数负，除数正）
         *
         * Runtime: 1 ms, faster than 99.98% of Java online submissions for Divide Two Integers.
         * Memory Usage: 36.3 MB, less than 27.88% of Java online submissions for Divide Two Integers.
         *
         * @param dividend
         * @param divisor
         * @return
         */
        public static int divideTwo(int dividend, int divisor) {
            if (dividend == divisor) return 1;
            if (dividend == Integer.MIN_VALUE && divisor == 1) return dividend;
            if (dividend == Integer.MIN_VALUE && divisor == Integer.MAX_VALUE) return -1;
            if (divisor == Integer.MAX_VALUE && divisor == -dividend) return -1;
            if (divisor == Integer.MAX_VALUE || divisor == Integer.MIN_VALUE) return 0;
            int result = 0;
            long[] array = new long[32];
            boolean isPos = (dividend > 0 && divisor > 0) || (dividend < 0 && divisor < 0);
            // 除数确保不会溢出了
            if (divisor < 0) divisor = -divisor;
            array[0] = divisor;
            for (int i = 1; i < array.length; i++) {
                array[i] = array[i - 1] << 1;
            }
            // 被除数如果是最小值要另外判断
            if (dividend == Integer.MIN_VALUE) {
                for (int i = array.length - 1; i >= 0; i--) {
                    if (dividend <= -array[i]) {
                        dividend += array[i];
                        result += 1 << i;
                        if (result<0) return Integer.MAX_VALUE;
                    }
                }
            } else {
                if (dividend < 0) dividend = -dividend;
                for (int i = array.length - 1; i >= 0; i--) {
                    if (dividend >= array[i]) {
                        dividend -= array[i];
                        result += 1 << i;
                    }
                }
            }
            if (isPos) return result;
            else return -result;
        }
    }
}

问题：不使用 * / % 符号完成除法

思路：1. 暴力算法，除法可以看作减法，每次减去被除数，当结果<0说明结束，但是这样会导致被除数为1的时候循环次数为被除数，会超时的

思路：2. 首先位运算 除2：>>1 乘2：<<1。然后我们看整个除法表达式，比如 13/4 = 3 ==> 13 = 4 * 3 换算成二进制：1101 = 4 * 0010+ 4* 0001 也就是4个 0010和0001，所以可以看出规律，那就是除法的结果必定为除数的倍数的二进制位。

由此可以遍历二进制数（从 1000.. 遍历到 000..001），题目的最大是32位，现在假如最高8位，那么从最高位开始 1000 0000 * 4 > 1010 循环直到发现0010(2) * 4 < 1101,记录下0010, 那么剩下是数就是 13-8=5 ,继续遍历0001 * 4 < 5 记录下0001，遍历结束，结果为 0001 *4 + 0010 * 4 即 0001 + 0010 （3） * 4 ，最后结果为 3。

具体实现中，为了不使用乘法符号完成乘法，使用<< 比如 0001和0010分别乘4就是 4 和 4<<1，所以可以定义一个初始数组arr，arr[0]放被除数，1,2,3 分别是前一位的乘2即<<1。

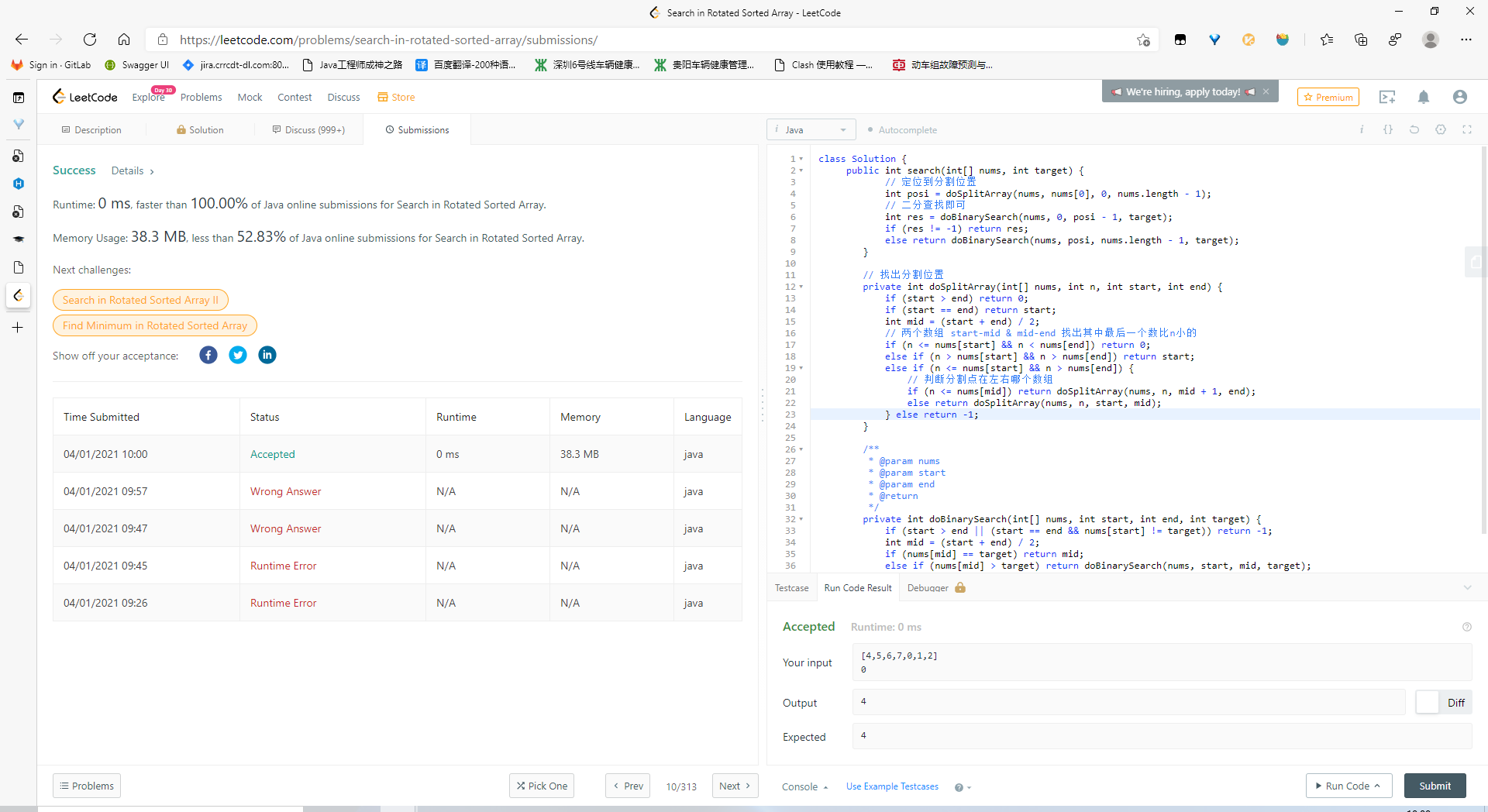
33 Search in Rotated Sorted Array M

这题应该挺简单的，不停二分就是了，既然100%了就不看官方答案了

 * 题目是给定一个未知的数，数组会根据这个数旋转，
 * For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].
 *
 * 思路：二分法，反正第一个数肯定是比最后一位大，数组二分，筛选出目标数组，第一个数比分组后的最后一个大就是目标数组，
 * 将目标数组再次二分，这个数再比对两个数组的最后一个数，找出最小的所在的数组，直到目标数组为1 记录下标，
 *
 * 找到记录下标后说明确定了分割位置，将数组分割成两个有序数组，然后二分查找即可

代码逻辑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
package com.leetcode;

import java.util.Arrays;

public class SearchInRotatedSortedArray33 {
    public static void main(String[] args) {
        System.out.println(new Solution().search(new int[]{ 1,3,5}, 1));
    }

    /**
     * 题目是给定一个未知的数，数组会根据这个数旋转，
     * For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].
     * <p>
     * 思路：二分法，反正第一个数肯定是比最后一位大，数组二分，筛选出目标数组，第一个数比分组后的最后一个大就是目标数组，
     * 将目标数组再次二分，这个数再比对两个数组的最后一个数，找出最小的所在的数组，直到目标数组为1 记录下标，
     * <p>
     * 找到记录下标后说明确定了分割位置，将数组分割成两个有序数组，然后二分查找即可
     *
     * Runtime: 0 ms, faster than 100.00% of Java online submissions for Search in Rotated Sorted Array.
     * Memory Usage: 38.3 MB, less than 52.83% of Java online submissions for Search in Rotated Sorted Array.
     * 
     */
    static class Solution {
        public int search(int[] nums, int target) {
            // 定位到分割位置
            int posi = doSplitArray(nums, nums[0], 0, nums.length - 1);
            // 二分查找即可
            int res = doBinarySearch(nums, 0, posi - 1, target);
            if (res != -1) return res;
            else return doBinarySearch(nums, posi, nums.length - 1, target);
        }

        // 找出分割位置
        private int doSplitArray(int[] nums, int n, int start, int end) {
            if (start > end) return 0;
            if (start == end) return start;
            int mid = (start + end) / 2;
            // 两个数组 start-mid & mid-end 找出其中最后一个数比n小的
            if (n <= nums[start] && n < nums[end]) return 0;
            else if (n > nums[start] && n > nums[end]) return start;
            else if (n <= nums[start] && n > nums[end]) {
                // 判断分割点在左右哪个数组
                if (n <= nums[mid]) return doSplitArray(nums, n, mid + 1, end);
                else return doSplitArray(nums, n, start, mid);
            } else return -1;
        }

        /**
         * @param nums
         * @param start
         * @param end
         * @return
         */
        private int doBinarySearch(int[] nums, int start, int end, int target) {
            if (start > end || (start == end && nums[start] != target)) return -1;
            int mid = (start + end) / 2;
            if (nums[mid] == target) return mid;
            else if (nums[mid] > target) return doBinarySearch(nums, start, mid, target);
            else return doBinarySearch(nums, mid + 1, end, target);
        }
    }
}

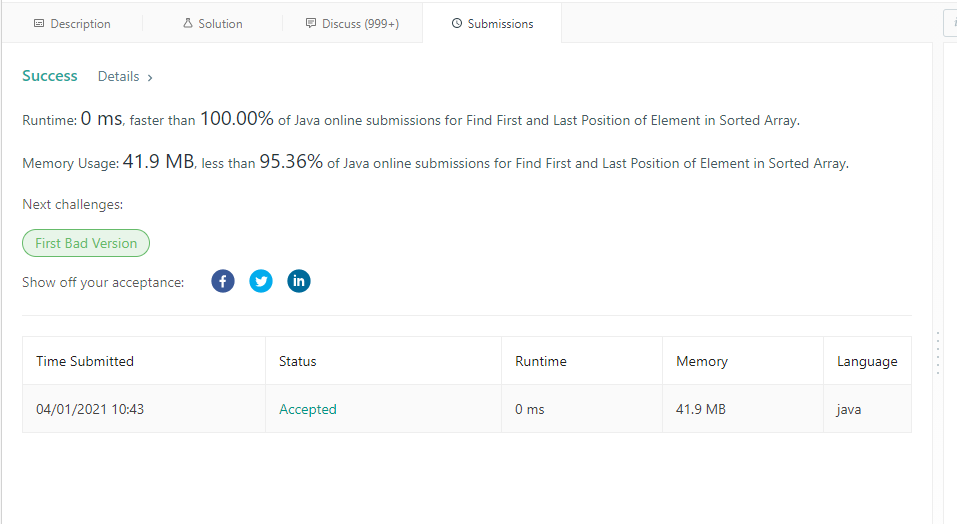
upload successful

34. Find First and Last Position of Element in Sorted Array M

二分就行的题目 ， 30分钟 100%+95%

  • 题目
    • 给定一个排序数组，找出目标的起始位置和终点位置下标
    • 思路：先定位到目标，然后从目标往前和往后看是否连续，记录最后一次连续下标
    • Given an array of integers nums sorted in ascending order, find the starting and ending position of a given target value.
    • If target is not found in the array, return [-1, -1].
    • Follow up: Could you write an algorithm with O(log n) runtime complexity?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
       public int[] searchRange(int[] nums, int target) {
            if (nums.length == 0) return new int[]{-1, -1};
            int res = binarySearch(nums, 0, nums.length - 1, target);
            if (res == -1) return new int[]{-1, -1};
            int s = res, e = res;
            // 往前查看连续
            while (s > 0 && nums[s] == nums[s - 1]) s--;
            // 往后查看
            while (e < nums.length - 1 && nums[e] == nums[e + 1]) e++;
            return new int[]{s, e};
        }

        private int binarySearch(int[] nums, int start, int end, int target) {
            if (start > end || (start == end && nums[start] != target)) return -1;
            int mid = (start + end) / 2;
            if (nums[mid] == target) return mid;
            else if (nums[mid] > target) return binarySearch(nums, start, mid, target);
            else return binarySearch(nums, mid + 1, end, target);
        }
}

upload successful

35. Search Insert Position easy

easy 题 没什么好说的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

package com.leetcode;

public class SearchInsertPosition35 {
    public static void main(String[] args) {
        System.out.println(new Solution().searchInsert(new int[]{1, 3, 5, 6}, 5));
    }

    /**
     * 问题：Given a sorted array of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.
     * Input: nums = [1,3,5,6], target = 2
     * Output: 1
     * <p>
     * 思路：不仅得找到下标，如果没找到还得找到应该插入的下标，二分法，直到start==end的时候判断 target<=nums[start]的话 返回start，否则返回 start-1
     */
    static class Solution {
        public int searchInsert(int[] nums, int target) {
            return doBinarySearch(nums, 0, nums.length - 1, target);
        }

        public int doBinarySearch(int[] nums, int start, int end, int target) {
            if (start > end) return -1;
            if (start == end) {
                if (target <= nums[start]) return start;
                else return start + 1;
            }
            int mid = (start + end) / 2;
            if (nums[mid]==target) return mid;
            else if (nums[mid] > target) return doBinarySearch(nums, start, mid, target);
            else return doBinarySearch(nums, mid + 1, end, target);
        }
    }
}

Welcome to my other publishing channels