FLOYD 最短路径算法
思路
佛洛依德最短路径实际上是使用了两个邻接矩阵遍历完成的 O(n^3),一个邻接矩阵A用来保存点到点的路径权重,另一个B用来保存路径。
A的初始已经写好了点到点的直接距离,对于没有直连的点,内容都算作无穷。然后依次取中间点后再依次遍历通过这个中间点的距离,如果小于原来的A矩阵的内的距离,那么就覆写且将路径写入B矩阵。
图解例子
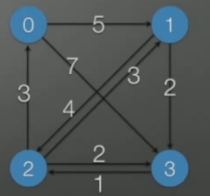
根据这个图做两个矩阵A(存储点到点的距离),B(存储经过点)
1
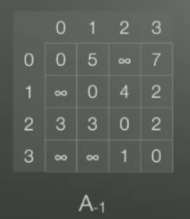
| 以上图为例,录入后的矩阵A,A[0][1]表示0节点到1节点的距离为5,A[1][0]就表示节点1到节点0的距离,无穷表示无法连接。
|

1
| 路径Path,对于B[0][1]表示 0节点到1节点需要经过什么节点
|
1
2
3
4
5
6
7
8
9
10
| 现在开始从头遍历,先找出节点对(就是图中什么节点可以到什么节点)有:
<0,1> <0,2> <0,3>
<1,0> <1,2> <1,3>
<2,0> <2,1> <2,3>
<3,0> <3,1> <3,2>
现在取中间节点0(挨个取0,1,2,3):对于0节点来说0节点到某节点距离,使用0作为中间节点是无意义的,所以包含0节点的节点对都不看,从<1,2>开始,即1使用0节点作为中间节点到2 = 1到0的节点距离+ 0到2的节点距离,也就是 A[1,2] = A[1,0] + A[0,2]。如果这个距离是小于原来距离的那么就更新,这里4>无穷所以不更新。
每次算可能有点绕,这里有个技巧:假设还是算 A[1,2]以 X 作为中间节点,可以先找到 A[1,2]在图中的点,分别朝着两个 X 方向走(X 行和 X 列),看他们的和是否小于自己,小于就更新自己,且在B矩阵内更新B[1,2] = X。这里X可以是0,1,2,3节点。
|
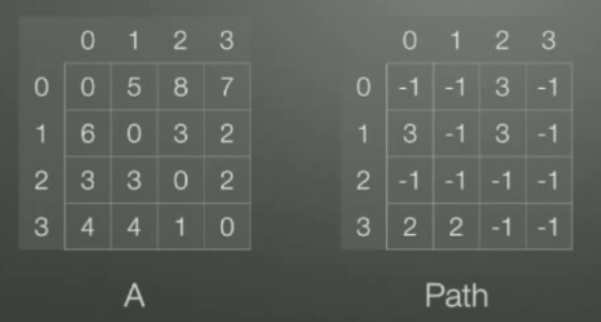
如此遍历更新两个矩阵得到最后结果:
查找代码实现
现在我们得到了最后的更新结果,使用的话以A[1][0]为例,即1节点到0节点从A矩阵可以看到1节点到0节点距离6,根据Path矩阵,看到Path[1][0] = 3表示 1到0节点要经过3,再看1到3和3到0,Path[1][3] = -1表示1到3直连,查Path[3][0] = 2 表示3到0经过节点2,查看3-2和2-0结果是-1,所以最后路径是1-3-2-0,不难发现这个过程是递归的,代码实现较为简单如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
void printPath(int x, int y, int matrixPath[][]) {
if (matrixPath[x][y] == -1) {
System.out.println("直连");
} else {
System.out.println("经过节点:" + matrixPath[x][y]);
printPath(x, matrixPath[x][y], matrixPath);
printPath(matrixPath[x][y], y, matrixPath);
}
}
|
最短路径实现
再看一下最短路径的过程会发现本质就是遍历更新两个表,从选取中间节点开始遍历,找到中间节点后遍历所有节点,对比节点的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
void floydGenerate(int matrix[][], int matrixPath[][]) {
for (int i = 0; i < matrixPath.length; i++) {
for (int j = 0; j < matrixPath.length; j++) {
matrixPath[i][j] = -1;
}
}
for (int passingByNode = 0; passingByNode < matrix.length; passingByNode++)
for (int startNode = 0; startNode < matrix.length; startNode++)
for (int endNode = 0; endNode < matrix.length; endNode++)
if (matrix[startNode][passingByNode] + matrix[passingByNode][endNode] < matrix[startNode][endNode]) {
matrix[startNode][endNode] = matrix[startNode][passingByNode] + matrix[passingByNode][endNode];
matrixPath[startNode][endNode] = passingByNode;
}
}
|



