Construct Binary Tree from Inorder and Postorder Traversal
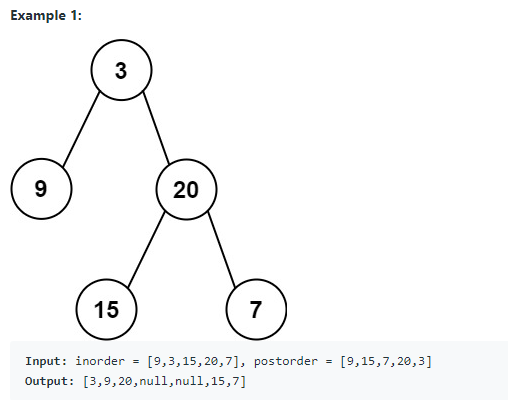
106 同 105一样 同样规则构建树,只不过计算左右集合时需要注意下! 55%
dp思路:和上一题一样 84, 转换下就好
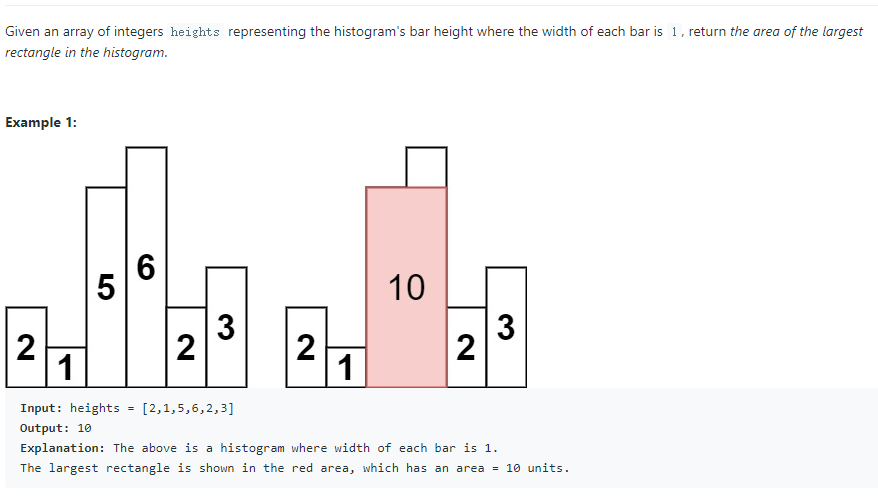
上一题的84题我实际用了递归和dp和这题不一样,这里的思路是:每个柱子的面积都是长度*高度,这个长度就是柱子右边的第一个小于柱子高度的柱子 - 柱子左边的第一个小于柱子高度的柱子 - 1,因此主要点在算长度。
这题的dp思想体现在算宽度,每层宽度可以通过上层算出。
1 |
|
1 | package com.leetcode; |
不难
1 |
|
快排 看到leetcode有类似快排的算法,0换到左边,2换到右边 懒得实现了
1 | private void doSort(int[] nums, int start, int end) { |
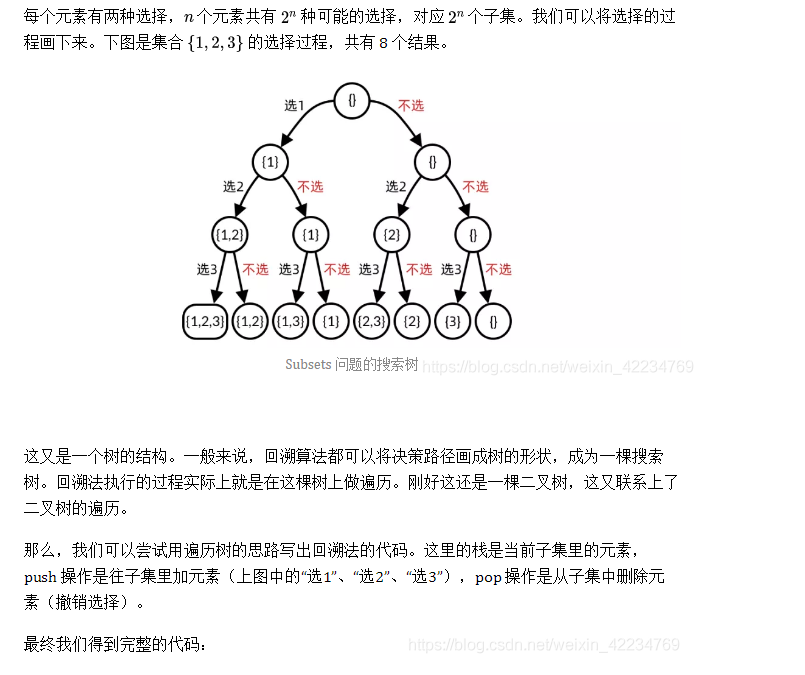
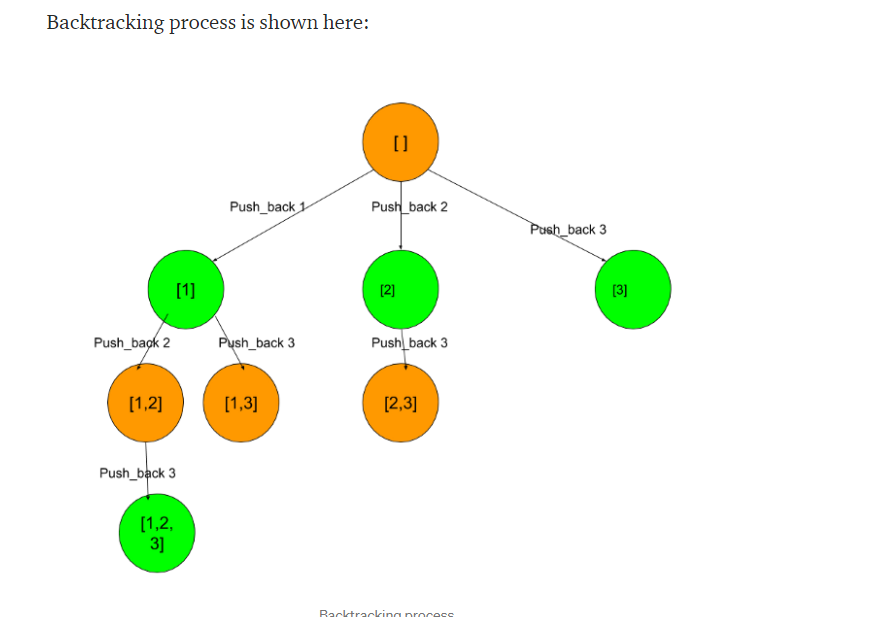
这个问题要好好看看的 新的套路或者说新的思想,两种回溯,一种是深度优先搜索
1 | package com.leetcode; |
思路:首先定位首字母,然后查找周围匹配的下一个字母,注意的是这里需要回溯,一条路走不通,可能另一条就可以。且每个字母不能被重复用,所以加一个数组用来标记
1 | package com.leetcode; |
1 | package com.leetcode; |
1 | package com.leetcode; |
hard 用了dp的思想,用数组存储了面积最大值,这个算法24ms,67%,有待优化
1 | package com.leetcode; |
easy

1 | package com.leetcode; |
难点在空间复杂度 O(1)
1 | package com.leetcode; |
需要注意的是 二分法找行的时候,如果行首数小于target,还要判断行尾数是否也小于target,都小于才能startRow = middleRow + 1
1 |
|
medium 动态规划题
一次ac

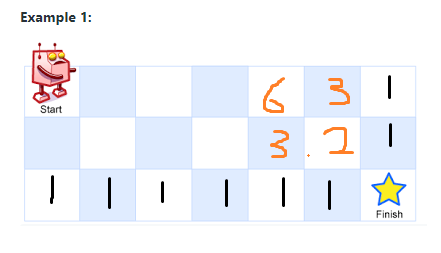
机器人只能向右和向下走,问走到终点几种方案,比较简单的经典动规
思路:在finish上方和左边到finish点个只有一种,记录下来,finish点左上方到达下面一个点是1种,到达右边也是一种,所以左上角到终点是1*1 + 1*1 = 2 种。所以对于每个点只要算上右边和下边的和就够了。
1 | package com.leetcode; |
在上题基础上加了障碍物
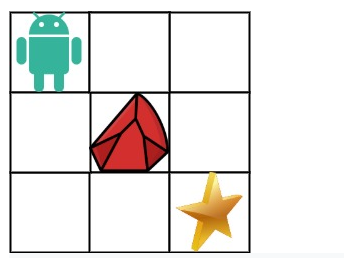
思路:还是和上题一样,只不过每个节点算下和右和的时候如果有障碍物不算进去
1 | leetcode 的eg真是佛了,还有输入{{0}}和{{1}},{{0,0},{0,1}}即起点在终点,终点被堵住这种情况。 |
1 | package com.leetcode; |

思路和上面两题一样 动规
1 | private static class Solution { |
三种解题方法和思路,最好的80%
1 | package com.leetcode; |
动规和贪心的解决方案
贪心算法:
1 | package com.leetcode; |
medium
1 | package com.leetcode; |